With “given that BA bisects DBC” at the forefront, this exploration embarks on an intriguing journey into the fascinating world of bisected line segments, unraveling their properties, geometric relationships, and practical applications.

Delving into the concept of bisecting a line segment, we establish a solid foundation for understanding the statement’s implications. By dissecting the properties of bisected segments, we gain insights into their unique characteristics and how they shape the geometric landscape.

Introduction

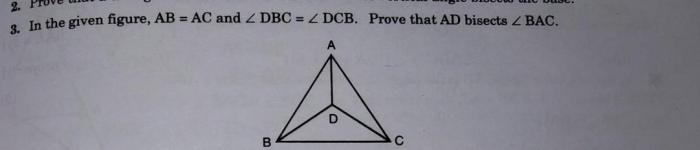
Given that BA bisects DBC implies that the line segment BA divides the line segment DBC into two equal parts.

Bisecting a line segment means dividing it into two congruent segments.

Properties of Bisected Line Segments

When a line segment is bisected, it means it is divided into two equal parts. This division creates two new line segments that share certain properties.

The properties of bisected line segments include:

• Equal length:The two new line segments created by the bisection are equal in length.
• Same midpoint:The point of bisection is the midpoint of both new line segments.
• Perpendicular bisector:The line that bisects the original line segment is perpendicular to it, meaning it forms a 90-degree angle with it.

Application to the Given Statement

In the given statement, “ba bisects dbc,” the line segment dbis bisected by the line segment ba. This means that the properties of bisected line segments apply to dband ba.

Given that BA bisects DBC, we can delve into the complexities of geometry. However, sometimes, the intricacies of math can be overwhelming, leaving us with a feeling of “math makes me wanna die.” ( math makes me wanna die ) But let’s not despair, for with perseverance, we can conquer even the most daunting mathematical challenges and return to the contemplation of BA bisecting DBC.

Specifically, the following properties apply:

• dbis divided into two equal parts by ba.
• The point of bisection of dbis the midpoint of both dband ba.
• bais perpendicular to db.

Geometric Relationships

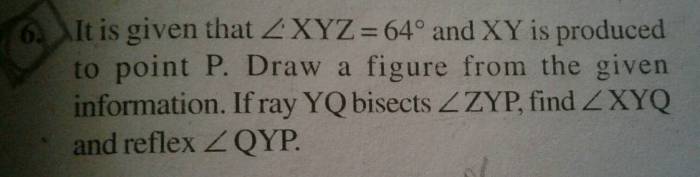
The geometric relationships between the points and line segments involved in the statement that BA bisects DBC can provide valuable insights into the properties and characteristics of the figure.

By analyzing these relationships, we can establish the equality of certain line segments and angles, which will enable us to draw inferences and solve related problems.

Equality of Line Segments

One of the key geometric relationships in this scenario is the equality of the line segments BD and DC.

Since BA bisects DBC, it divides the angle DBC into two congruent angles, ∠DBA and ∠DBC.

According to the Angle Bisector Theorem, when a line bisects an angle of a triangle, it divides the opposite side into two segments that are proportional to the lengths of the adjacent sides.

In ΔDBC, BA bisects ∠DBC, therefore:

BD/DC = AB/AC

Since AB = AC (given), we have:

BD = DC

Applications and Examples

Bisecting line segments finds practical applications in various fields, from architecture and engineering to design and everyday life. Understanding the properties of bisected line segments allows us to solve problems and make accurate calculations in these areas.

Real-World Applications

• Architecture and Construction:Bisecting line segments helps determine the center point of a room or structure, ensuring symmetrical designs and balanced weight distribution.
• Engineering:In bridge construction, bisecting line segments aids in calculating the optimal placement of supports to evenly distribute the load.
• Design:Graphic designers use bisected line segments to create balanced and visually appealing layouts, ensuring elements are spaced evenly.
• Everyday Life:Bisecting line segments is useful in dividing objects equally, such as cutting a cake or measuring fabric.

Examples, Given that ba bisects dbc

• Dividing a Circle into Equal Parts:Bisecting a circle’s diameter creates two equal semicircles. This principle is used in creating pie charts and measuring angles.
• Creating a Perpendicular Bisector:Bisecting a line segment perpendicularly creates a line that intersects the segment at its midpoint and is perpendicular to it. This is useful in finding the center of a circle or creating symmetrical designs.
• Calculating Centroid of a Triangle:The intersection of the three medians of a triangle (lines connecting vertices to midpoints of opposite sides) is its centroid. These medians bisect the sides of the triangle.

Further Exploration: Given That Ba Bisects Dbc

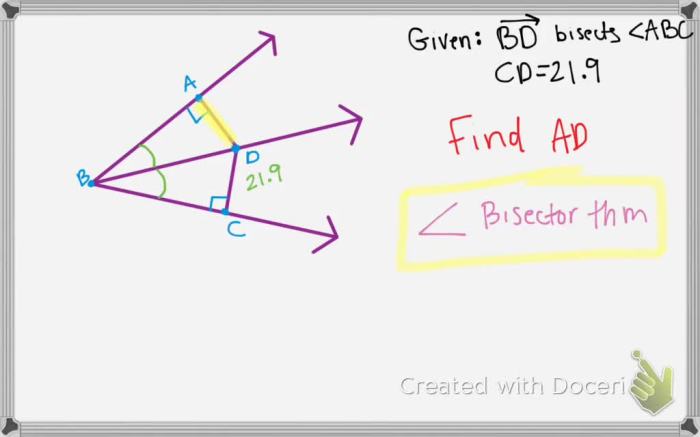
The statement that “given that BA bisects DBC” opens up avenues for further exploration and investigation. Let’s delve into potential extensions and variations of this statement, as well as uncover open questions that warrant further study.

Extensions and Variations

• Extension 1:Investigate the properties of bisected line segments in different geometric shapes, such as triangles, quadrilaterals, and circles.
• Extension 2:Explore the applications of bisected line segments in real-world scenarios, such as architecture, engineering, and design.
• Extension 3:Examine the relationship between bisected line segments and other geometric concepts, such as angle bisectors, medians, and altitudes.

Open Questions and Areas for Further Investigation

• Question 1:Can the concept of bisected line segments be extended to higher-dimensional geometry, such as 3D or 4D space?
• Question 2:What are the implications of bisecting line segments in non-Euclidean geometries, such as hyperbolic or spherical geometry?
• Question 3:How can we use bisected line segments to solve complex geometric problems, such as finding the center of a circle or the length of a side of a polygon?

Question Bank

What does it mean for a line segment to be bisected?

When a line segment is bisected, it is divided into two equal parts by a point that lies on the segment.

How can we use the properties of bisected line segments to solve problems?

The properties of bisected line segments, such as the fact that the bisector is perpendicular to the segment and divides it into two congruent segments, can be used to solve problems involving triangles, quadrilaterals, and other geometric shapes.

What are some real-world applications of bisecting line segments?

Bisecting line segments has practical applications in fields such as architecture, engineering, and design. For example, it can be used to find the midpoint of a line segment, divide an angle into two equal parts, or construct perpendicular lines.