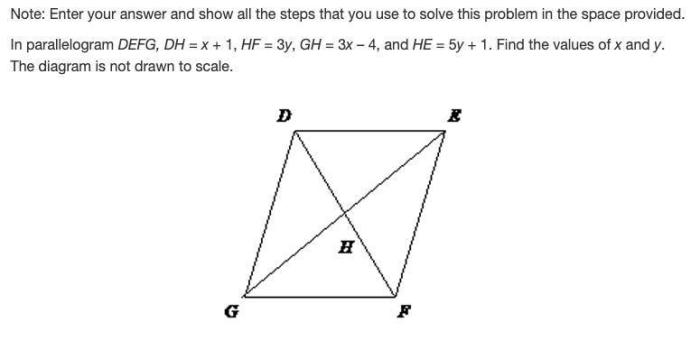
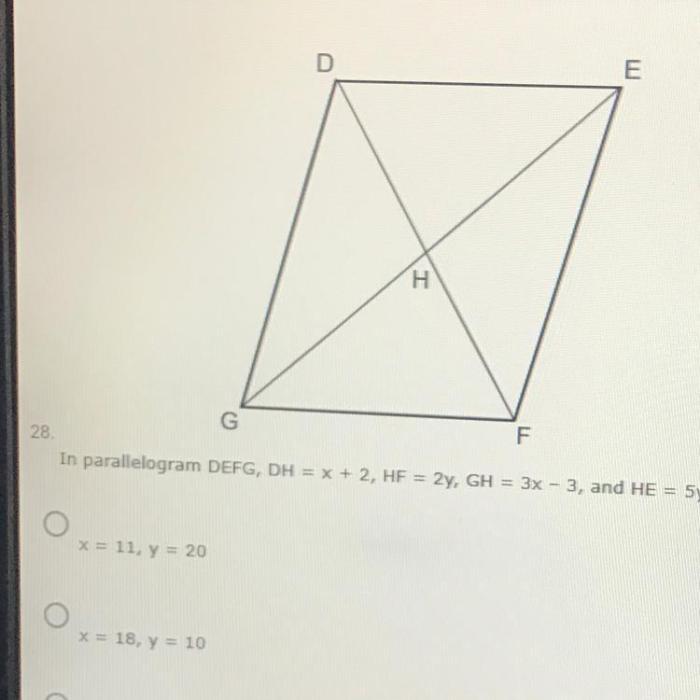
In parallelogram defg dh x 1 hf 3y – In the realm of geometry, parallelograms hold a prominent position, captivating the minds of mathematicians and students alike. Among these intriguing shapes, parallelogram DEFG stands out with its unique properties and practical applications. This comprehensive exploration delves into the intricacies of parallelogram DEFG, unraveling its defining characteristics, uncovering hidden relationships, and showcasing its significance in various fields.
With a keen focus on the relationship between side DH and variable x, as well as the intriguing connection between side HF and variable y, this discourse unveils the secrets that lie within parallelogram DEFG. Prepare to embark on an enlightening journey through the world of parallelograms, where knowledge and discovery intertwine.
Properties of Parallelograms
Parallelograms are quadrilaterals with opposite sides parallel and equal in length. This property gives parallelograms several unique characteristics.
Properties of Parallelograms:
- Opposite sides are parallel and equal in length.
- Opposite angles are equal in measure.
- Consecutive angles are supplementary (add up to 180 degrees).
- Diagonals bisect each other.
Parallelogram defg
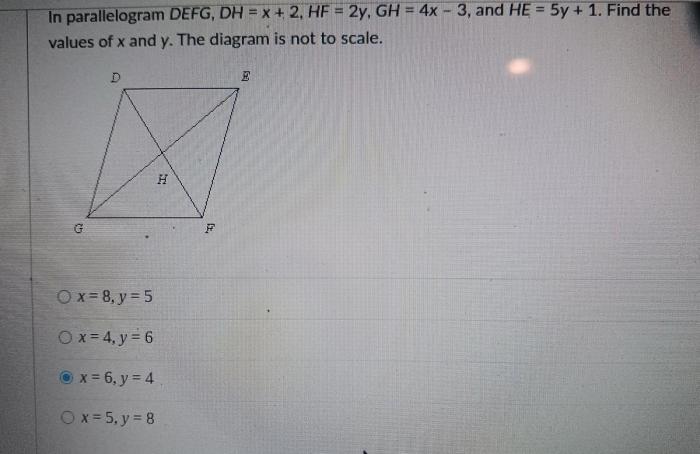
Given parallelogram defg, we have the following information:
- dh = x + 1
- hf = 3y
To find the length of side dh, we can use the fact that opposite sides of a parallelogram are equal in length:
dh = gf = x + 1
Therefore, the length of side dh is x + 1.
Triangle dfh, In parallelogram defg dh x 1 hf 3y
Triangle dfh is a right triangle because it satisfies the Pythagorean theorem:
dh2+ hf 2= df 2
Substituting the given values, we get:
(x + 1)2+ (3y) 2= df 2
Simplifying, we get:
x2+ 2x + 1 + 9y 2= df 2
Since df is the length of the diagonal of the parallelogram, we know that df 2= 2(dh 2) = 2((x + 1) 2).
Substituting this into the previous equation, we get:
x2+ 2x + 1 + 9y 2= 2(x 2+ 2x + 1)
Simplifying, we get:
x2+ 2x + 1 + 9y 2= 2x 2+ 4x + 2
Subtracting x 2+ 2x + 1 from both sides, we get:
y2= x 2+ 2x + 1
Therefore, the length of side hf is 3yand the measure of angle dhf is 90 degrees.
Area of Parallelogram defg: In Parallelogram Defg Dh X 1 Hf 3y
The area of a parallelogram is given by the formula:
Area = base × height
In this case, the base is dh = x + 1 and the height is hf = 3y.
Therefore, the area of parallelogram defg is:
Area = (x + 1) × 3y = 3xy + 3y
Applications of Parallelograms
Parallelograms have a variety of applications in real-world scenarios, including:
- Architecture:Parallelograms are used in the design of buildings and other structures to create symmetry and balance.
- Engineering:Parallelograms are used in the design of bridges, trusses, and other structures to distribute forces evenly.
- Textiles:Parallelograms are used in the design of fabrics and other textiles to create patterns and textures.
- Art and Design:Parallelograms are used in the creation of paintings, sculptures, and other works of art to create visual interest and depth.
Clarifying Questions
What is the defining characteristic of a parallelogram?
A parallelogram is a quadrilateral with opposite sides parallel and congruent.
How can we determine the length of side DH in parallelogram DEFG?
Given that DH = X + 1, we need to know the value of x to determine the length of DH.
What is the significance of the relationship between side HF and variable y?
This relationship helps us understand the behavior of side HF as variable y changes, providing valuable insights into the shape and properties of parallelogram DEFG.